「インフル陽性です!」は正しいか?
そろそろ東京でもインフルエンザが風物詩になる季節になろうとしています。
今回、インフルエンザ迅速検査について書いてみようかと思います。
偽陰性と偽陽性
インフルエンザ検査もすべての検査も言えるのですが、百発百中ではありません。本当は病気なのに陰性と出る例(偽陰性)と病気ではないのに陽性に出る例(偽陽性)が出る場合があります。これを表にするとこんなかんじです。
| 病気あり | 病気なし | 計 | |
|---|---|---|---|
| 検査陽性 | a | b | a+b |
| 検査陰性 | c | d | c+d |
| 計 | a+c | b+d | a+b+c+d |
ここで、bが偽陽性でcが偽陰性です。
感度と特異度
優秀な検査は、bもcも少ないものです。これを式で表したのが、感度と特異度です。
感度=a/a+c (病気な人 a+c を病気であると言える割合)
特異度=d/b+d (病気ではない人 b+d を病気でないといえる割合)
です。インフルエンザ迅速検査の場合、特異度は高めですが、感度は発熱してからの時期・採取方法(喉・鼻の奥・鼻水)などで結構違います。当然のことなら、発熱してからすぐに検査しても、感度は下がります。詳しくは、製薬会社のサイトになりますがインフルエンザ迅速診断キットも参考にしてみてください。
ここで問題なってくるのは、インフルエンザ迅速検査をして陽性だった場合、果たして本当のインフルエンザだろうか?ということです。なんだか頓珍漢な質問をしているように思えるかもしれませんが、上の表を見れば検査陽性でも実は病気ではない人(偽陽性)の人がいることがわかります。
陽性的中率
「検査が陽性だった人の中 a+b で、本当に病気な人 a がどのくらいいるか」を表す式を陽性的中率といいます。
陽性的中率=a/a+b
偽陽性(b)の人たちが本当に病気にかかって検査陽性(a)の人たちよりも多くなれば(陽性的中率が半分以下)、これは検査として役に立たないことがわかります。
この陽性的中率は病気になっている人の割合(有病率 a+c/a+b+c+d)で大きく変わってきます。計算してみましょう。
有病率50%の場合の陽性的中率
ここで、10000人がいて病気の人が半分(有病率50%)とします。検査の感度・特異度をそれぞれ90%とすると
| 病気あり | 病気なし | 計 | |
|---|---|---|---|
| 検査陽性 | 4500 | 500 | 5000 |
| 検査陰性 | 500 | 4500 | 5000 |
| 計 | 5000 | 5000 | 10000 |
となり、陽性的中率は90%です。
有病率1%の場合の陽性的中率
今度は有病率を1%ほどにします。同じ条件で計算すると
| 病気あり | 病気なし | 計 | |
|---|---|---|---|
| 検査陽性 | 90 | 990 | 1080 |
| 検査陰性 | 10 | 8910 | 8920 |
| 計 | 100 | 9900 | 10000 |
となり、陽性的中率は8.3%です。検査陽性でも、91.7%の確率で偽陽性(つまりインフルエンザではない)のです。あまり検査をする気になれませんね。
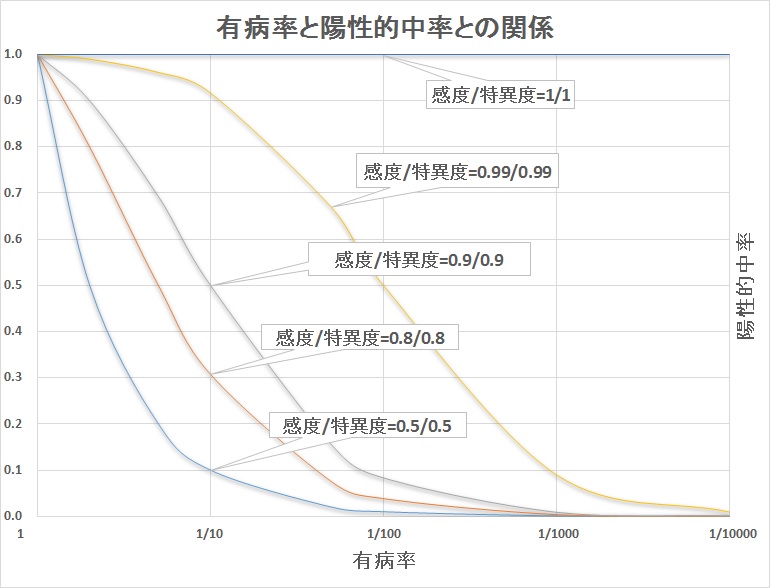
有病率と陽性的中率
有病率と陽性的中率の関係をグラフにしてみました。感度/特異度が高くても有病率が下がれば、陽性的中率は下がるのがわかります。
別の言い方をすれば「非常に珍しい病気であれば、どんなに優れた検査法でも病気ではない人を陽性と判定しまうことが多くなる」です。
おまけ
事前確率と事後確率
ちょっと別の考え方で有病率50%の場合、検査しない場合はインフルエンザの確率が50%(事前確率)だけど検査をして陽性が出たことで90%に上がった(事後確率)という考え方もできます。これをベイズ統計学といいます。
詳しく知りたい人は、佐藤吉宗先生の統計学入門(1)-偽陽性問題-を読んでみてください。
臨床症状によって事後確率は変わります
有病率1%の場合は、インフルエンザ検査陽性で事後確率は8.3%に上がります。ただ、急激な発熱・悪寒(さむけ)・筋肉痛・身内がインフルエンザなどという条件があれば、それだけ事後確率が上がります。要は「臨床的診断」です。多くの医師は、検査結果陽性だけで判断するものではないということは心に留めておいて下さい。
逆にインフルエンザ迅速検査が陰性でも、各種臨床症状が伴えば臨床的にインフルエンザと診断することもあります(陰性的中率が低い)。
おまけ2(タミフルを出さない医者)
昨冬書いた当院ブログも読んで下さい。
a:75420 t:3 y:4